Le niveau à bulle est un dispositif hydrostatique destiné à vérifier l'horizontalité d'une surface. On peut le simuler très facilement avec un dispositif qui possède
- un écran (pour dessiner la bulle)
- un accéléromètre (pour connaître le vecteur à afficher)
Or le Sense Hat et les tablettes tactiles possèdent ces deux outils, et le nano-projet présenté ici consistera juste à lire les coordonnées du champ gravitationnel pour les afficher à l'écran. En effet, ce champ est un vecteur vertical g, dont les coordonnées valent environ (0;0;-9,8) et si l'appareil est vertical, sa projection sur la tablette doit être le vecteur nul (bulle au centre de l'écran). Cependant, si on penche la tablette vers la gauche, la projection de ce vecteur sur la tablette aura une abscisse négative (du moins en mode "paysage") ce qui ferait aller la bulle vers la gauche si on ne gardait que l'abscisse et l'ordonnée de g: En fait, lorsque le niveau à bulle est incliné vers la gauche, l'eau descend et la bulle monte. Donc pour savoir où dessiner la bulle, on
- lit les coordonnées (x,y,z) de g, via l'accéléromètre
- garde seulement x et y vu que l'écran est en 2D
- change leur signe pour que la bulle monte au lieu de descendre
- dessine la bulle sous la forme d'un cercle de rayon constant et centré sur (x,y) ou plutôt sur (kx,ky) où k est un nombre négatif destiné à rendre l'appareil réaliste (pas trop sensible par exemple)
Sur le Sense Hat, on a un problème supplémentaire: Pas facile de dessiner un disque sur une matrice de 64 LEDs. Alors on le fait flou, sur 2 pixels de rayon, avec une formule trouvée par essais et erreurs. En plus, on quitte le programme dès que la bulle arrive au bord de la matrice de LEDs pour éviter les messages d'erreurs. Cela se fait avec une variable booléenne on_continue, par défaut à "true" (pour qu'on continue) et on boucle tant qu'elle est à "true". Quand la bulle arrive au bord de l'écran, on positionne cette variable à "false" pour quitter la boucle:
from sense_hat import SenseHat
sense = SenseHat()
on_continue = True
while on_continue:
vecteur = sense.get_accelerometer_raw()
x = -vecteur['x']*2 + 3.5
y = -vecteur['y']*2 + 3.5
for i in range(8):
for j in range(8):
n = int(100*max(2-(i-x)**2-(j-y)**2,0))
sense.set_pixel(i,j,n,n,n)
if (x-4)**2>20 or (y-4)**2>20:
on_continue = False
Avec 13 lignes de Python, c'est même petit pour un mini-projet.
Il reste donc un peu de place pour montrer comment des élèves d'ICN (ou d'ISN) peuvent rapidement programmer un niveau à bulle pour leur propre smartphone. C'est aussi facile que sur le Sense Hat, grâce à app inventor, qui permet de créer des applications Android en déplaçant des blocs comme Scratch et Blockly. L'application étant elle-même en ligne, il est envisageable de créer une application Android sur la tablette directement. Cependant, un ordinateur est quand même bien pratique. Pour tester l'appli, il est pratique d'installer sur un smartphone de test, l'application ai companion, qui remplace l'émulateur et accélère considérablement la phase de test. Donc, pour créer un niveau à bulle Android, on va sur le site app Inventor (à l'aide de Chrome et en se connectant depuis son compte gmail...), et on démarre un nouveau projet. La première phase de conception ressemble à un travail de webmestre: Placer des éléments à l'écran et leur donner un identifiant. Les éléments sont choisis dans la palette, et sont de trois types:
- un rectangle (noir) remplissant l'écran (type "canvas")
- un lutin en forme de disque (cyan) placé dans le rectangle, et capable de bouger (ici en modifiant ses coordonnées); de type "ball"
- et un senseur (accéléromètre) invisible à l'écran
Le deux premiers éléments sont dans la palette graphique; on les rajoute à l'écran par cliquer-glisser (le canvas sur l'écran, le ball sur le canvas):
Et le dernier élément est dans la palette "sensors"; on le glisse n'importe où sur l'écran virtuel vu qu'il sera en dehors de cet écran:
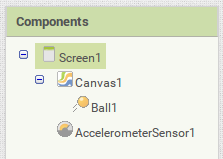
La structure de l'écran devrait donc être celle-ci pour un niveau à bulle:
En cliquant sur un des éléments, on peut modifier, tout à droite de la page, ses propriétés (taille couleur titre etc) dans la fenêtre "éléments". L'apprentissage de css est un atout pour cette phase. L'écran peut avoir, avec quelques réglages de ce genre, cet aspect:
On a donc déjà une idée de ce que ça donne avant même d'allumer le smartphone de test. Noter que ci-dessus l'écran a été positionné en mode "portrait" ce qui va nécessiter d'échanger les coordonnées x et y, parce que le repère n'est pas le même pour l'écran et l'accéléromètre, du moins en mode portrait. Le test en temps réel avec le companion est pratique pour trouver comment donner un mouvement cohérent à la bulle. C'est en cliquant sur "blocks" qu'on commence à programmer, et il y a deux choses à faire:
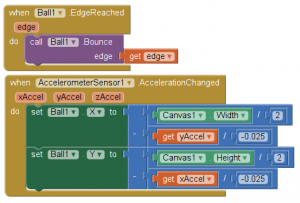
- gérer les sorties d'écran (demander à la bulle de rebondir si elle arrive au bord de l'écran)
- déplacer la bulle à chaque relecture des coordonnées de g
Voici l'intégralité du code source de ce niveau à bulle d'air:
Pour effectuer les tests, il faut allumer le smartphone (ou la tablette) Android (l'appareil sur lequel le companion a été installé), puis, en haut d'app Inventor, se connecter sur le companion (par la wifi donc il faut désactiver le mode avion):
Ceci a pour effet de faire apparaître un code de 6 lettres à entrer sur le smartphone, ainsi qu'un QR-code à flasher pour avoir automatiquement le code de 6 lettres. Ensuite, à chaque modification d'un bloc, le smartphone se met à jour et on voit immédiatement l'effet de la modification en live.
Quand on trouve l'application suffisament au point, on peut l'exporter:
Ceci a pour effet de placer dans le dossier "téléchargement" un fichier apk, qui peut ensuite être installé sur les smartphones des amis, parents etc.
Mais ce n'est pas tout: Comme avec Scratch, il est possible de partager ses projets (des fichiers xml avec l'extension "aia") sur le site du MIT, et de "remixer" ses propres projets ou ceux des autres abonnés au site. Le niveau à bulle d'air par exemple se trouve ici.